01、图

厨子大约 13 分钟数据结构算法基础面试题解析图程序厨校招社招

哈喽，大家好，我是厨子，今年给大家聊聊图

图是计算机科学中最重要的数据结构之一，它能够描述复杂的关系网络，从社交网络到交通系统，从编译器的依赖分析到搜索引擎的网页排名，图无处不在。

图的基本概念

图的定义和生活中的图

图（Graph）是由顶点（Vertex）集合和边（Edge）集合组成的数据结构，用来表示对象之间的关系。

数学定义： 图 G = (V, E)，其中：

V 是顶点集合，V = {v₁, v₂, ..., v_n}
E 是边集合，E = {e₁, e₂, ..., e_m}

生活中的图：

社交网络

顶点：每个人
边：朋友关系

城市交通网

顶点：城市
边：交通路线

程序调用关系

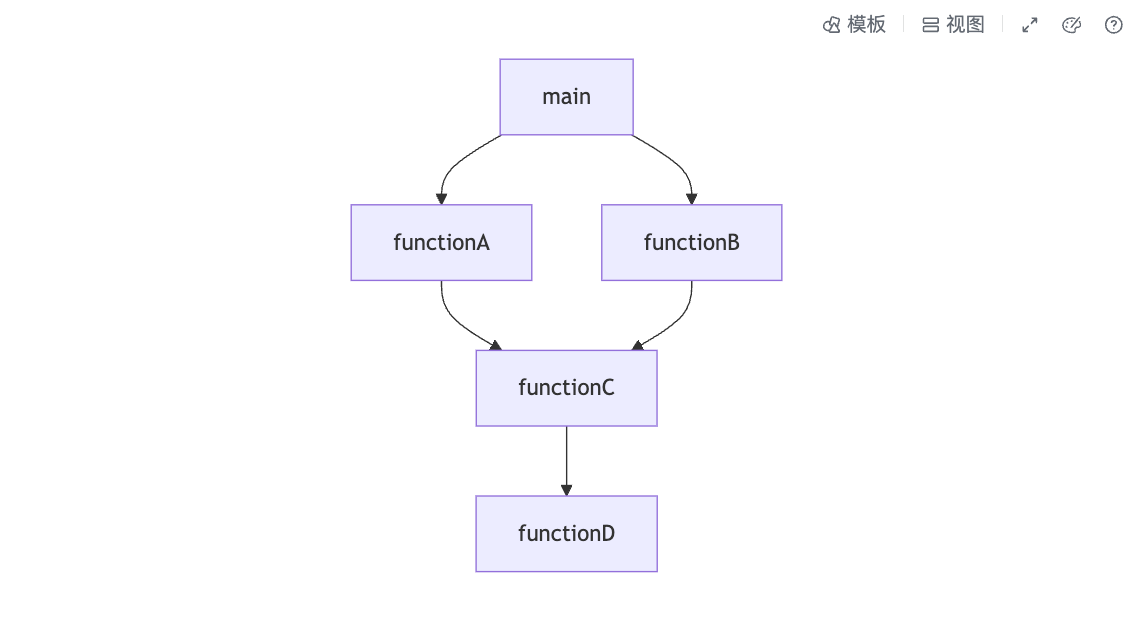
顶点：函数
边：调用关系

图的基本术语

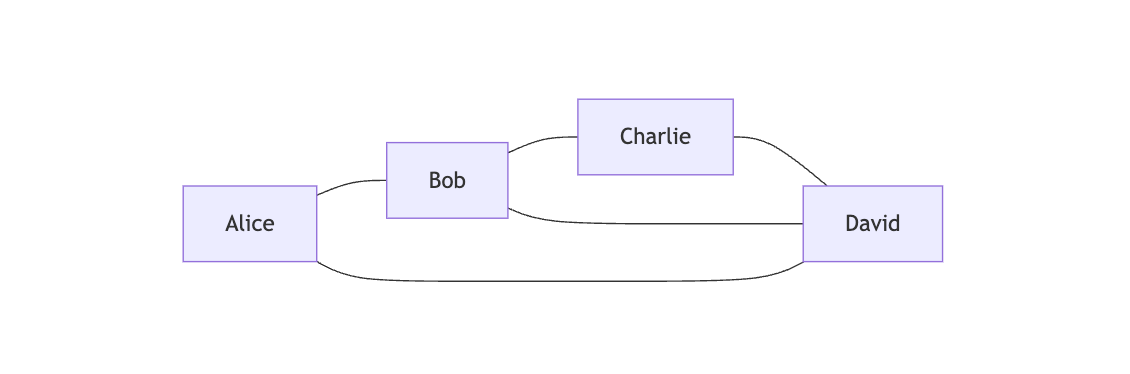
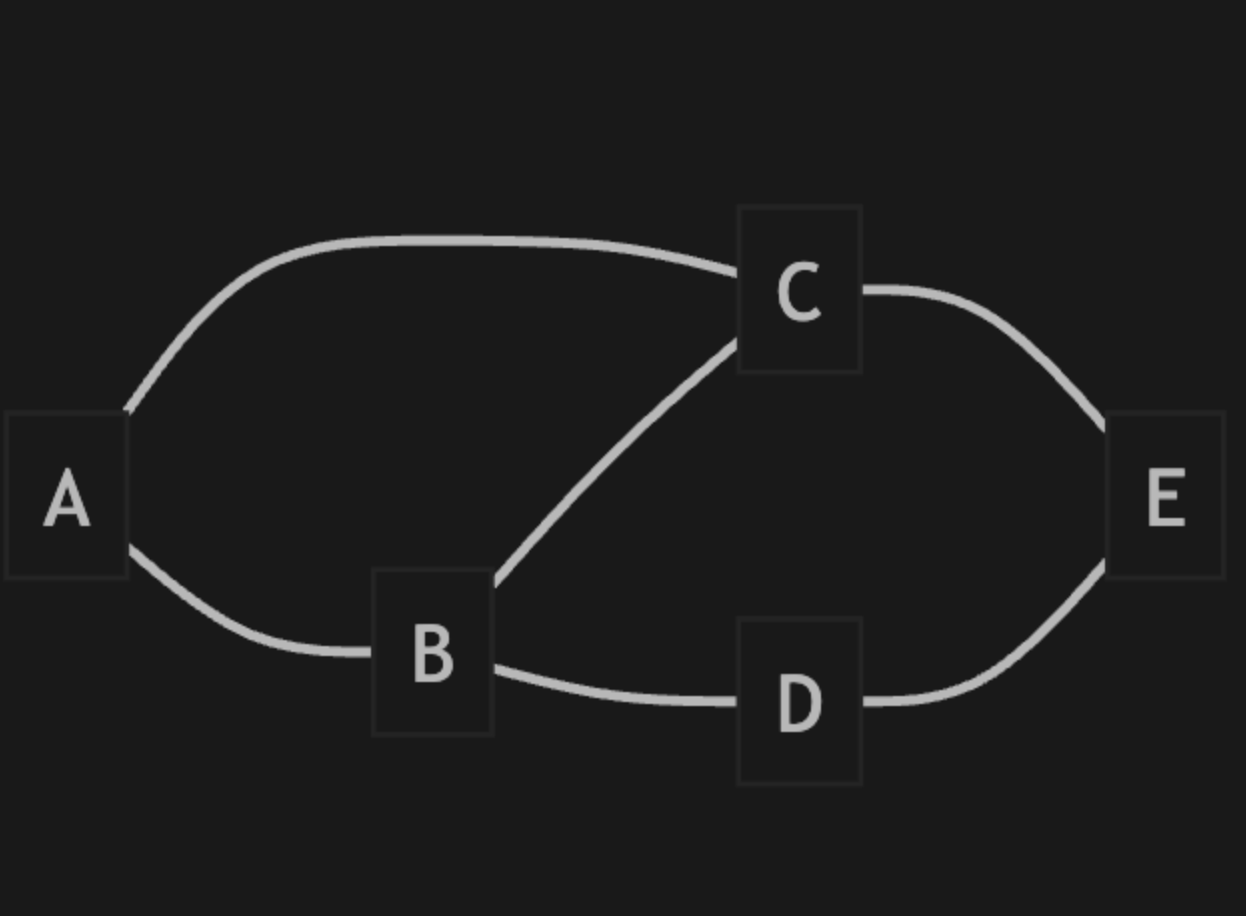
让我们通过一个具体的图来理解各种术语：

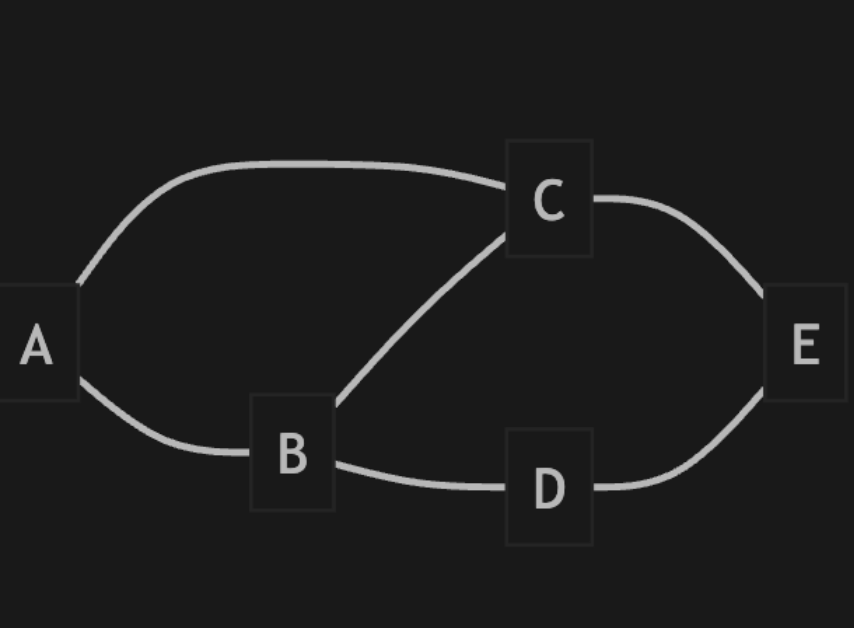
基本术语：

1. 顶点（Vertex/Node）

图中的基本单元，如上图中的 A, B, C, D, E

2. 边（Edge）

连接两个顶点的线，表示顶点间的关系

也就是上面的 AB，BC

3. 度（Degree）

与顶点相连的边的数量
上图中：deg(A) = 2, deg(B) = 3, deg(C) = 3, deg(D) = 2, deg(E) = 2

4. 路径（Path）

从一个顶点到另一个顶点经过的顶点序列
例如：A → B → D → E 是从 A 到 E 的一条路径

5. 路径长度

路径中边的数量
A → B → D → E 路径的长度为 3

6. 简单路径

除起点和终点外，不重复经过任何顶点的路径

7. 环（Cycle）

起点和终点相同的简单路径
例如：A → B → C → A

8. 连通性

如果两个顶点之间存在路径，则称它们是连通的

C++中的基本定义（等学会了如何存储图再回过头来看）：

#include <iostream>
#include <vector>
#include <string>


// 基本的图术语示例
class GraphTerms {
public:
    struct Vertex {
        int id;
        std::string name;
        std::vector<int> adjacentVertices;  // 邻接顶点列表

        Vertex(int i, std::string n) : id(i), name(n) {}

        // 计算度数
        int getDegree() const {
            return adjacentVertices.size();
        }
    };

    std::vector<Vertex> vertices;

    // 添加顶点
    void addVertex(int id, std::string name) {
        vertices.emplace_back(id, name);
    }

    // 添加边（无向图）
    void addEdge(int v1, int v2) {
        if (v1 < vertices.size() && v2 < vertices.size()) {
            vertices[v1].adjacentVertices.push_back(v2);
            vertices[v2].adjacentVertices.push_back(v1);
        }
    }

    // 打印图的基本信息
    void printGraphInfo() {
        std::cout << "图的基本信息：" << std::endl;
        std::cout << "顶点数量: " << vertices.size() << std::endl;

        int totalEdges = 0;
        for (const auto& vertex : vertices) {
            totalEdges += vertex.getDegree();
        }
        std::cout << "边数量: " << totalEdges / 2 << std::endl;  // 无向图每条边被计算两次

        std::cout << "\n各顶点的度数：" << std::endl;
        for (const auto& vertex : vertices) {
            std::cout << vertex.name << " (ID: " << vertex.id << "): 度数 = "
                 << vertex.getDegree() << std::endl;
        }
    }
};

// 使用示例
void demonstrateBasicTerms() {
    GraphTerms graph;

    // 添加顶点
    graph.addVertex(0, "A");
    graph.addVertex(1, "B");
    graph.addVertex(2, "C");
    graph.addVertex(3, "D");
    graph.addVertex(4, "E");

    // 添加边
    graph.addEdge(0, 1);  // A-B
    graph.addEdge(0, 2);  // A-C
    graph.addEdge(1, 2);  // B-C
    graph.addEdge(1, 3);  // B-D
    graph.addEdge(2, 4);  // C-E
    graph.addEdge(3, 4);  // D-E

    graph.printGraphInfo();
}

int main() {
        demonstrateBasicTerms();
        return 0;
}

图与其他数据结构的区别

与线性结构的区别：

特性	数组/链表	树	图
结构特点	线性序列	层次结构	网状结构
元素关系	前驱后继关系	父子关系	任意关系
连接数量	最多2个	父节点1个，子节点多个	任意数量
环的存在	无	无	可能有
遍历复杂度	O(n)	O(n)	O(V+E)

那我们来总结一下图的优势呢？

图的优势：

表达能力强：能表示复杂的多对多关系
应用广泛：网络、社交、地图、依赖关系等

所以图在实际开发中，应用场景也是蛮丰富的

示例对比：

// 线性结构：数组表示学生成绩
int scores[] = {85, 92, 78, 96, 88};

// 层次结构：树表示组织架构，父节点，子节点
class TreeNode {
public:
    string position;
    vector<TreeNode*> subordinates;
};

// 网状结构：图表示城市交通网
class CityGraph {
public:
    struct City {
        string name;
        vector<pair<City*, int>> connections;  // 连接的城市和距离
    };
    vector<City> cities;
};

我们了解了基本概念之后，我们来看下图的分类吧

图的分类

有向图 vs 无向图

无向图（Undirected Graph）

边没有方向性
边表示双向关系
如果存在边(u,v)，则也存在边(v,u)，他们是 完全相同的一条边

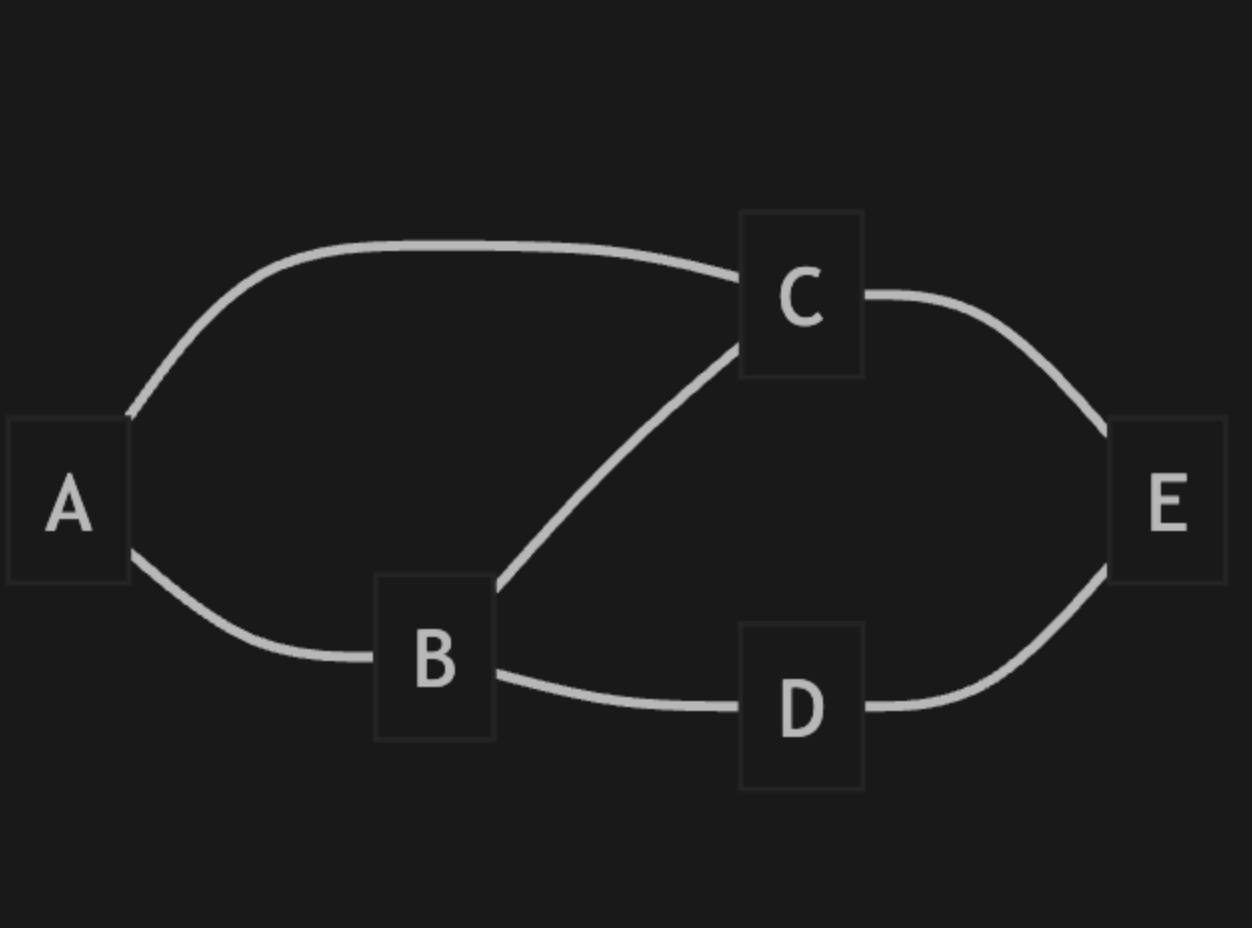
刚才提到的这个图就是无向图

有向图（Directed Graph/Digraph）

边有方向性
用箭头表示方向
边(u,v)和边(v,u)是不同的，因为此时边具有方向性

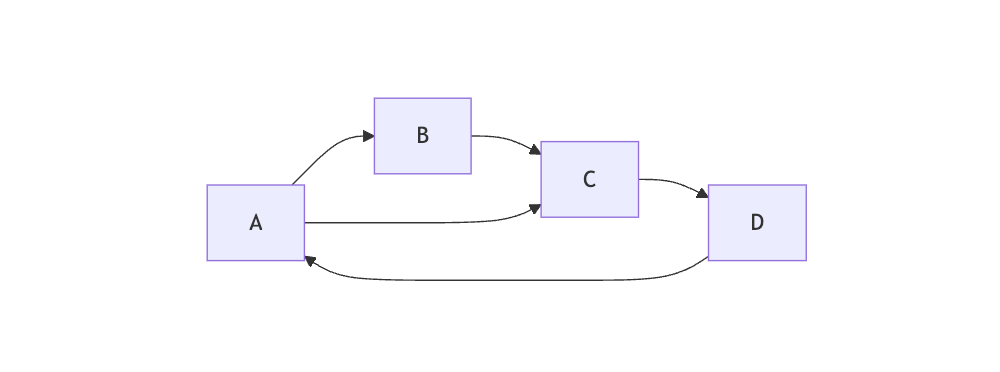
加权图 vs 无权图

无权图（Unweighted Graph）

边只表示连接关系
所有边的"权重"都相同（通常视为1）

加权图（Weighted Graph）

边带有权重值
权重可以表示距离、成本、容量等

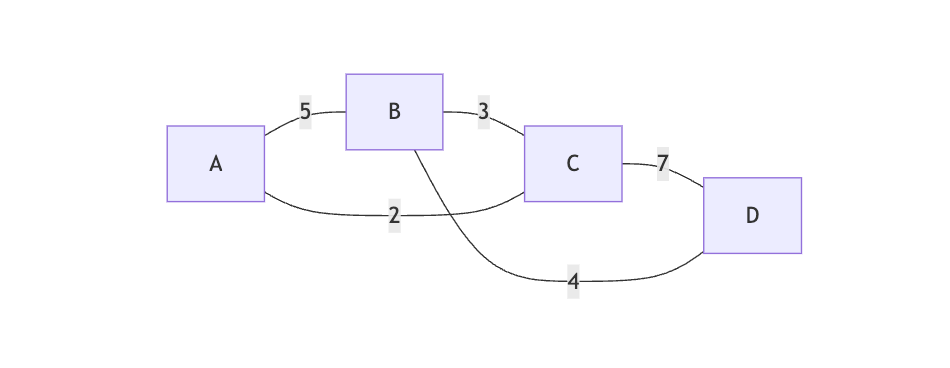
连通图 vs 非连通图

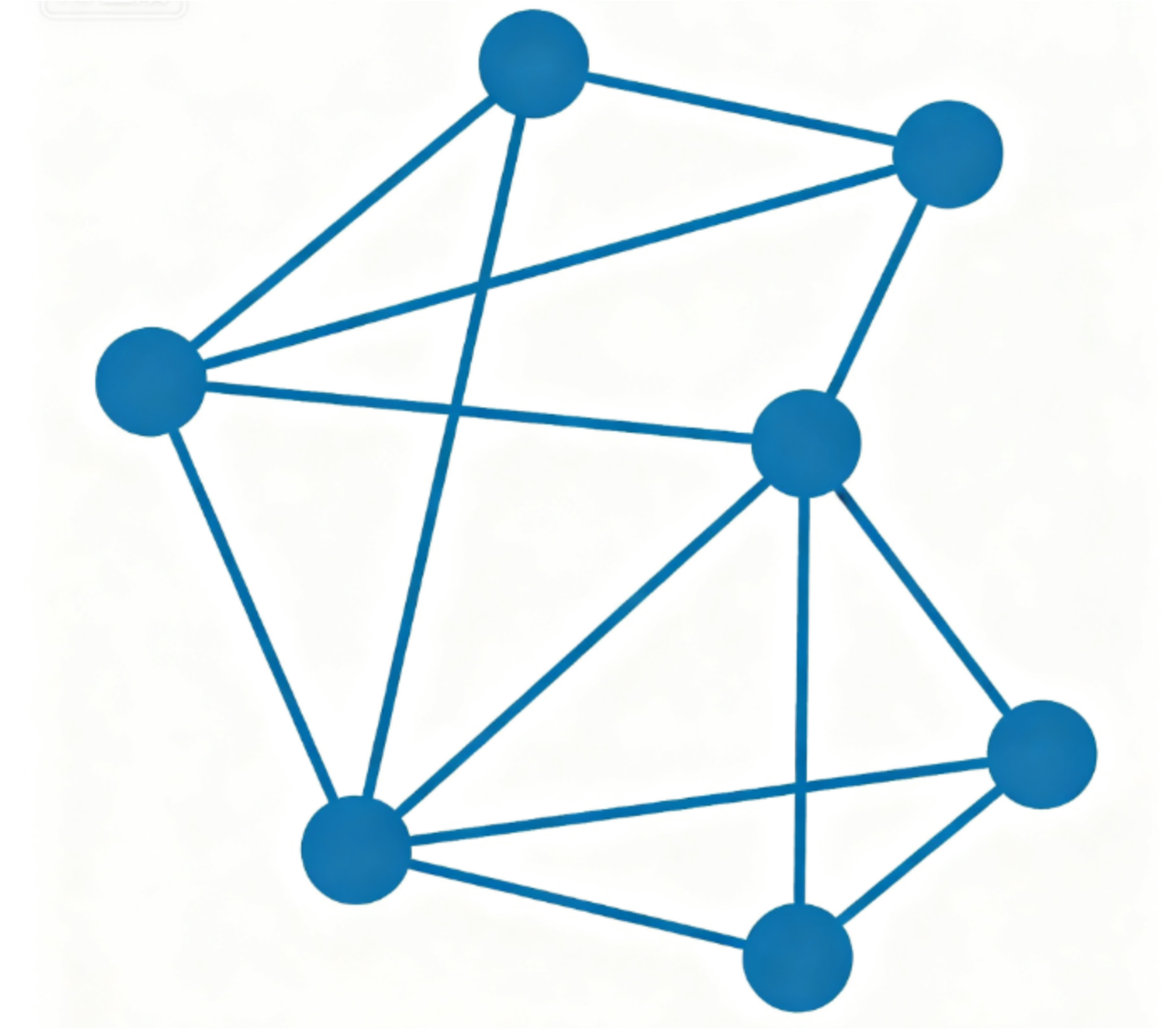
连通图（Connected Graph）

任意两个顶点之间都存在路径
整个图是一个连通分量

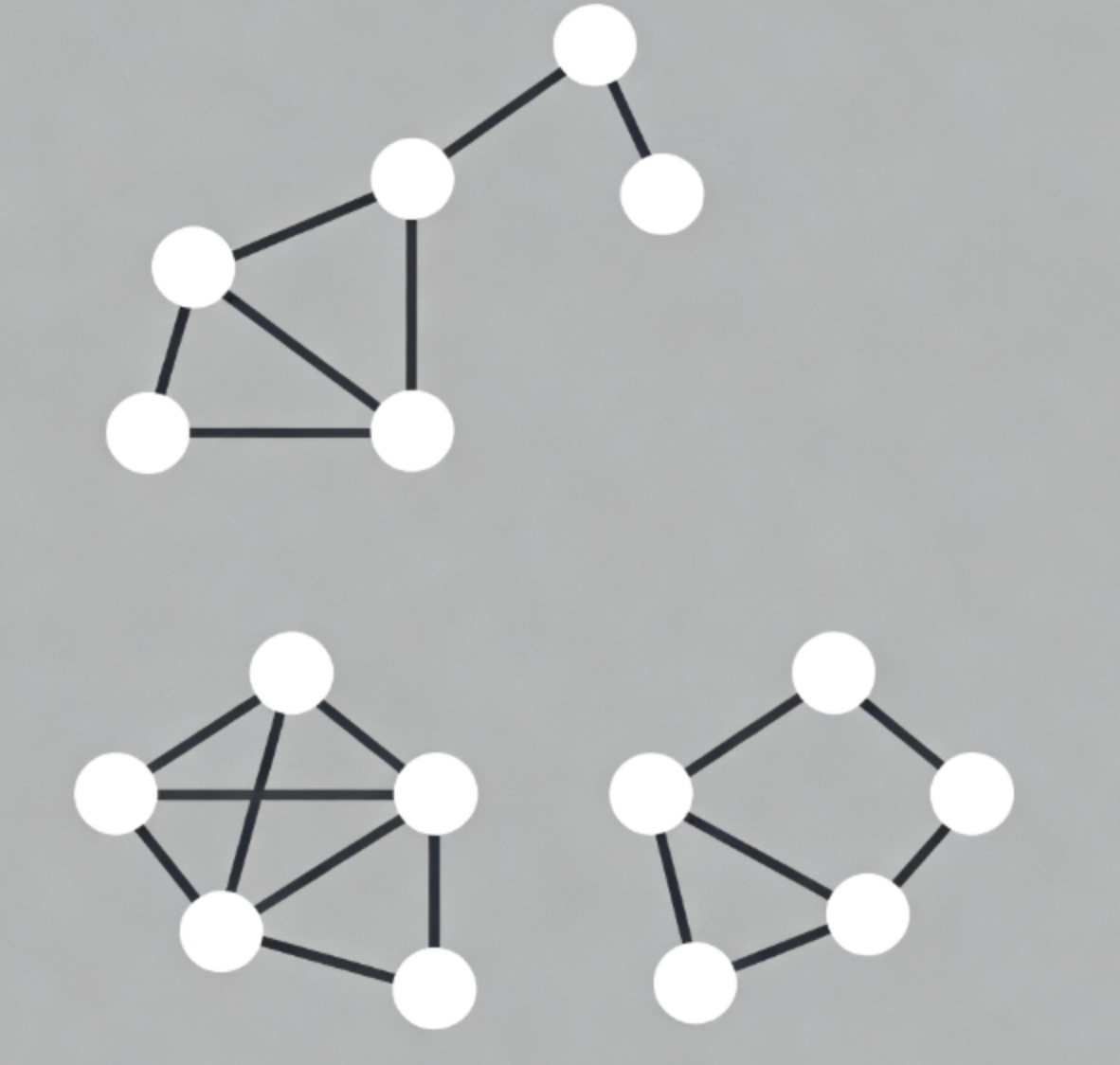
非连通图（Disconnected Graph）

存在某些顶点对之间没有路径
由多个连通分量组成

基本概念大家已经掌握了，现在给大家说一下特殊类型的图

特殊类型的图

完全图（Complete Graph）

完全图具有以下特性

任意两个不同顶点之间都有边相连
n个顶点的完全图有 n(n-1)/2 条边（无向完全图）

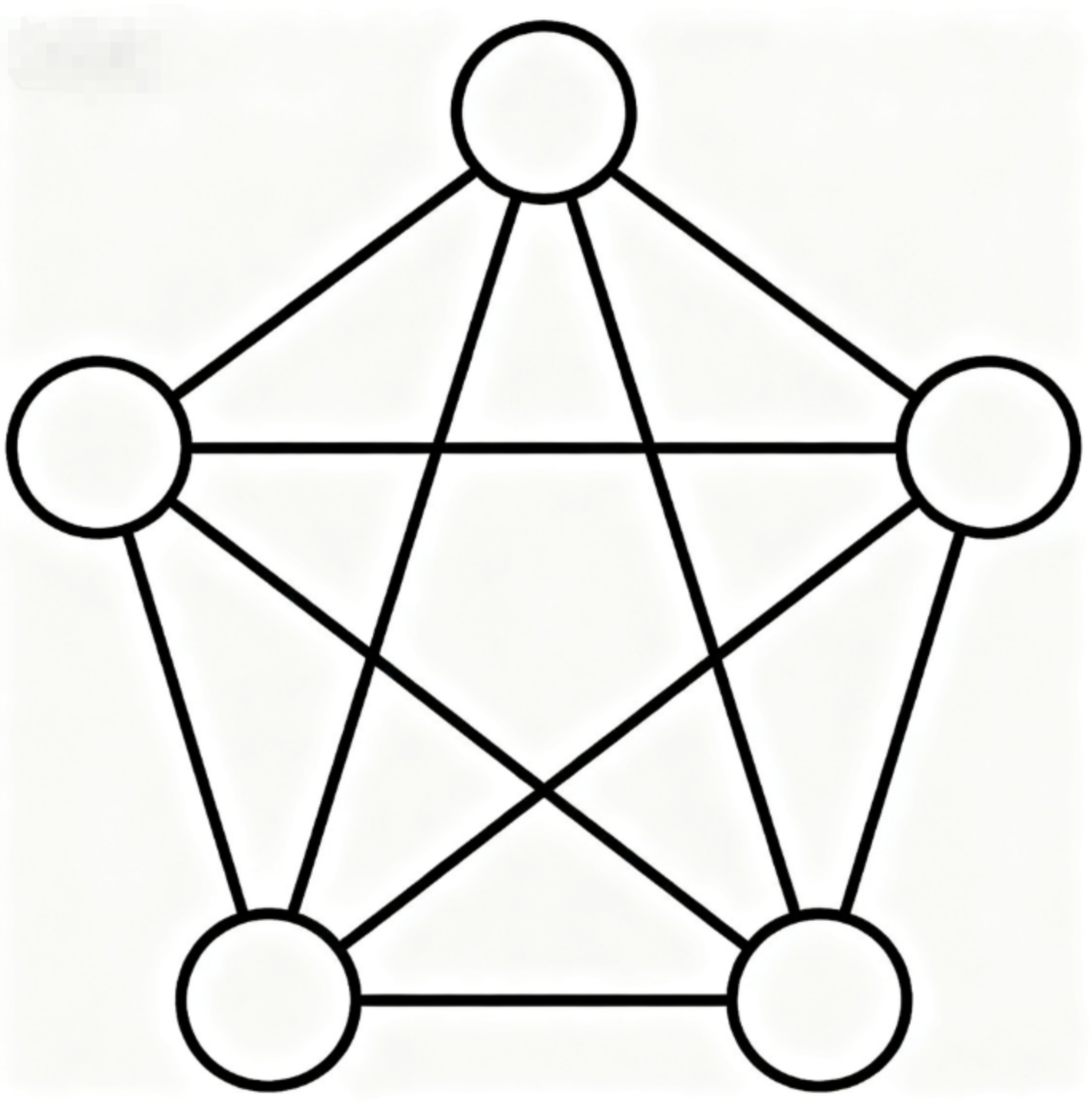
上图可以看到，每个顶点都有通向其他顶点的边

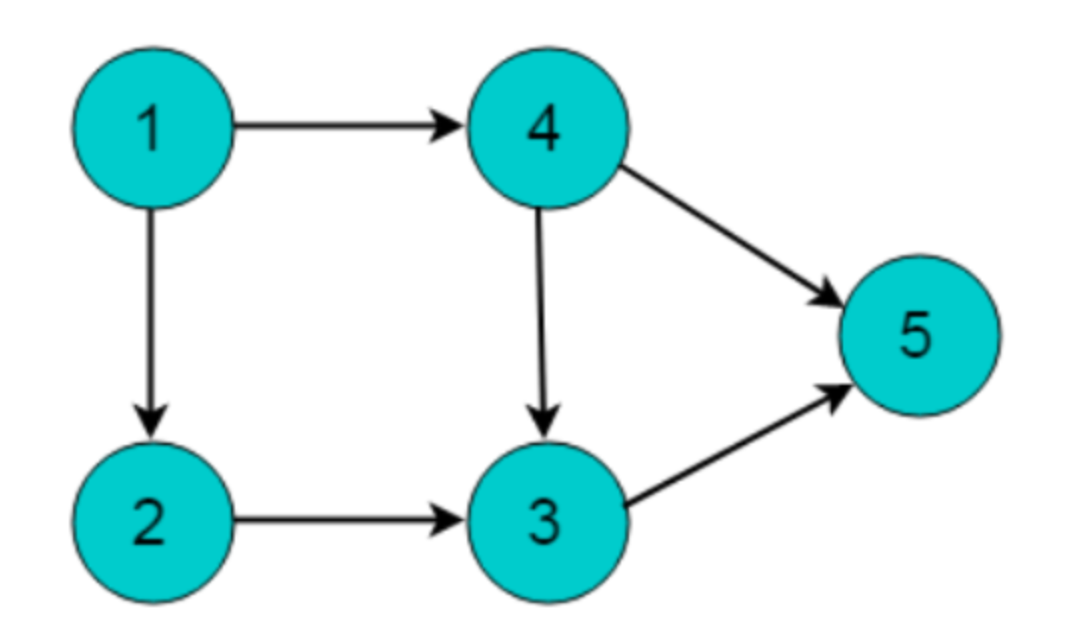
有向无环图（DAG - Directed Acyclic Graph）

有向图且无环（无法回到起点），该图常用于任务调度、依赖关系等，我们直接看示例

说完了图的基本概念，下面我们来说一下图的存储，这个也是非常重要的知识点

邻接矩阵存储

邻接矩阵的基本概念

邻接矩阵（Adjacency Matrix）是用二维数组来表示图的一种方法。对于有n个顶点的图，邻接矩阵是一个n×n的矩阵。

基本原理：

矩阵中的元素 matrix[i][j] 表示顶点i到顶点j的关系

对于无权图：1表示有边，0表示无边

对于加权图：存储边的权重

下面表格用来模拟一个 5X5 的二维数组，那在邻接矩阵中则存储为

A，B，C，D，E 节点在数组中对应的存储位置为 0，1，2，3，4

我们以节点 A举例，他有到 B 和 C 的边，没有到 D E 的边，那么 matrix[0][1] = 1 , matrix[0][2] = 1, matrix[0][3] = 0, matrix[0][4] = 0

邻接矩阵的实现方式

基础无权图实现：

class AdjacencyMatrix {
private:
    int numVertices;
    vector<vector<int>> matrix;

public:
    // 构造函数
    AdjacencyMatrix(int vertices) : numVertices(vertices) {
        matrix.resize(vertices, vector<int>(vertices, 0));
    }

    // 添加边（无向图）
    void addEdge(int source, int destination) {
        if (isValidVertex(source) && isValidVertex(destination)) {
            matrix[source][destination] = 1;
            matrix[destination][source] = 1;  // 无向图对称
        }
    }

    // 添加有向边
    void addDirectedEdge(int source, int destination) {
        if (isValidVertex(source) && isValidVertex(destination)) {
            matrix[source][destination] = 1;
        }
    }

    // 删除边（无向图）
    void removeEdge(int source, int destination) {
        if (isValidVertex(source) && isValidVertex(destination)) {
            matrix[source][destination] = 0;
            matrix[destination][source] = 0;
        }
    }

    // 检查边是否存在
    bool hasEdge(int source, int destination) {
        if (isValidVertex(source) && isValidVertex(destination)) {
            return matrix[source][destination] == 1;
        }
        return false;
    }

    // 获取顶点的度数（无向图）
    int getDegree(int vertex) {
        if (!isValidVertex(vertex)) return -1;

        int degree = 0;
        for (int i = 0; i < numVertices; i++) {
            if (matrix[vertex][i] == 1) {
                degree++;
            }
        }
        return degree;
    }

    // 获取顶点的出度（有向图）
    int getOutDegree(int vertex) {
        if (!isValidVertex(vertex)) return -1;

        int outDegree = 0;
        for (int i = 0; i < numVertices; i++) {
            if (matrix[vertex][i] == 1) {
                outDegree++;
            }
        }
        return outDegree;
    }

    // 获取顶点的入度（有向图）
    int getInDegree(int vertex) {
        if (!isValidVertex(vertex)) return -1;

        int inDegree = 0;
        for (int i = 0; i < numVertices; i++) {
            if (matrix[i][vertex] == 1) {
                inDegree++;
            }
        }
        return inDegree;
    }

    // 获取所有邻接顶点
    vector<int> getNeighbors(int vertex) {
        vector<int> neighbors;
        if (!isValidVertex(vertex)) return neighbors;

        for (int i = 0; i < numVertices; i++) {
            if (matrix[vertex][i] == 1) {
                neighbors.push_back(i);
            }
        }
        return neighbors;
    }

    // 打印邻接矩阵
    void printMatrix() {
        cout << "邻接矩阵：" << endl;
        cout << "   ";
        for (int i = 0; i < numVertices; i++) {
            cout << i << " ";
        }
        cout << endl;

        for (int i = 0; i < numVertices; i++) {
            cout << i << ": ";
            for (int j = 0; j < numVertices; j++) {
                cout << matrix[i][j] << " ";
            }
            cout << endl;
        }
    }

    // 统计边的总数
    int getEdgeCount() {
        int edgeCount = 0;
        for (int i = 0; i < numVertices; i++) {
            for (int j = i + 1; j < numVertices; j++) {  // 只计算上三角，避免重复
                if (matrix[i][j] == 1) {
                    edgeCount++;
                }
            }
        }
        return edgeCount;
    }

    int getVertexCount() const {
        return numVertices;
    }

private:
    bool isValidVertex(int vertex) {
        return vertex >= 0 && vertex < numVertices;
    }
};

邻接矩阵的空间和时间复杂度分析

空间复杂度：O(V²)

需要一个V×V的二维数组
无论图中实际有多少条边，都需要V²的空间
对于稀疏图（边数远小于V²）来说，空间浪费严重

时间复杂度分析：

操作	时间复杂度	说明
添加边	O(1)	直接设置矩阵元素
删除边	O(1)	直接重置矩阵元素
查找边	O(1)	直接访问矩阵元素
获取所有邻接顶点	O(V)	遍历一行
获取顶点度数	O(V)	遍历一行或一列
图的遍历	O(V²)	需要检查每个矩阵元素

根据上面的内容，大家对邻接矩阵，掌握应该比较清晰了，咱们来看一下邻接矩阵的优缺点吧

邻接矩阵的优缺点

优点：

快速查询：检查两个顶点是否相邻只需O(1)时间
简单实现：数据结构简单，易于理解和实现
适合稠密图：当图的边数接近V²时，空间利用率高
支持快速计算：便于进行矩阵运算，如计算可达性
删除顶点简单：删除一行一列即可

缺点：

空间浪费：对于稀疏图，大量存储空间被浪费
遍历效率低：获取所有邻接顶点需要O(V)时间
添加顶点困难：需要重新分配更大的矩阵
不适合动态图：顶点数量变化时效率低

邻接表存储

邻接表的基本概念

邻接表（Adjacency List）是图的另一种重要存储方式。它为每个顶点维护一个链表（或动态数组），存储该顶点的所有邻接顶点。

是不是看着有点抽象？嗯，我觉得也有点，我们直接来看个图吧

上面这个图，我们用邻接表存储的话，应该怎么存储呢？

基本原理：

使用一个数组存储所有顶点
每个顶点对应一个链表，链表中存储与该顶点相邻的所有顶点
对于加权图，链表中还需要存储边的权重

邻接表可以使用数组、链表、vector，这块我们画个示意图，大家就一目了然了

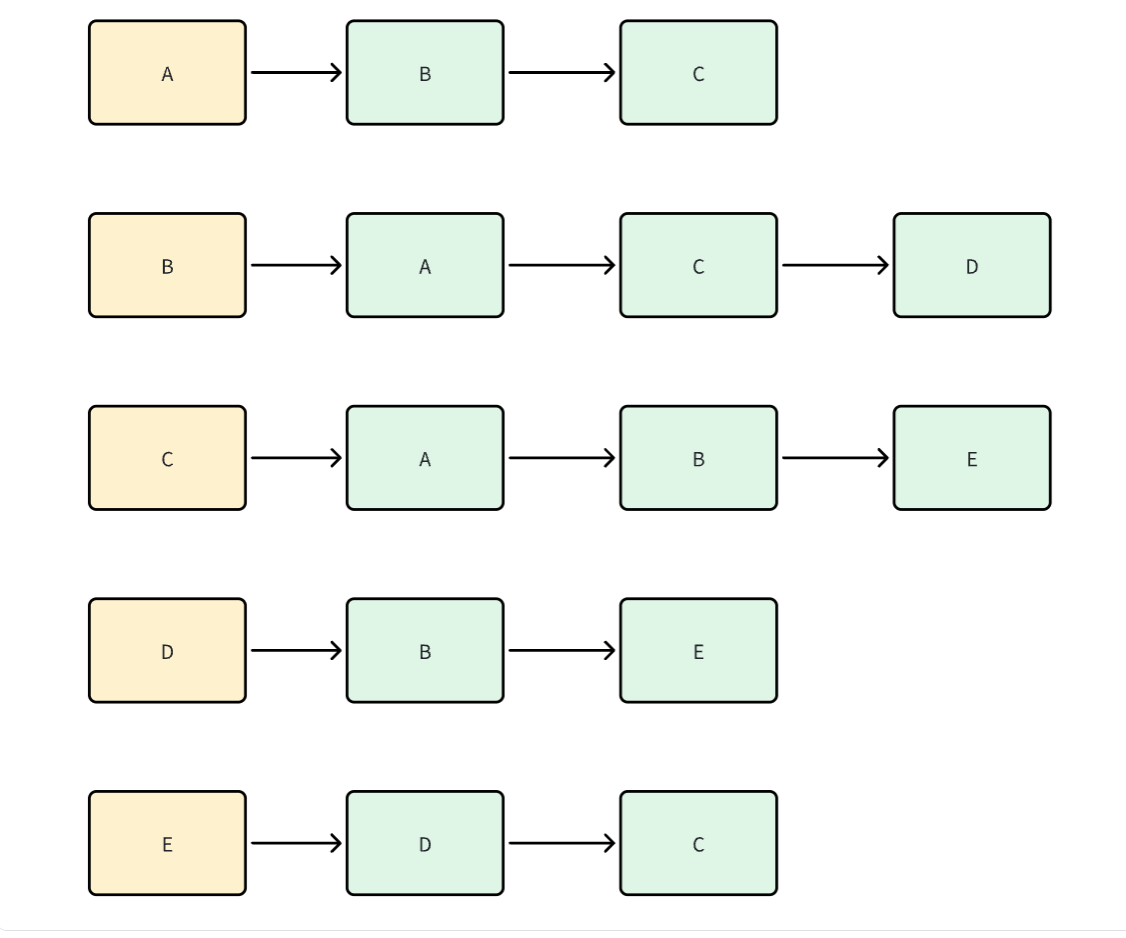
这里黄色的代表起点，绿色代表和其有链接的点，通过邻接表来存储图的话，则是一个复合数据结构

例如

 vector<vector<int>> adjList;
 vector<ListNode*> adjList;

邻接表的空间和时间复杂度分析

空间复杂度：O(V + E)

需要存储V个顶点
每条边在邻接表中被存储一次（有向图）或两次（无向图）
对于稀疏图非常节省空间

时间复杂度分析：

操作	时间复杂度	说明
添加边	O(1)	在链表头部或vector末尾添加
删除边	O(V)	需要在邻接表中查找
查找边	O(V)	最坏情况需要遍历整个邻接表
获取所有邻接顶点	O(度数)	直接返回邻接表
获取顶点度数	O(1)	返回邻接表大小
图的遍历	O(V + E)	访问每个顶点和边一次

邻接表 vs 邻接矩阵对比

详细对比分析：

特性	邻接矩阵	邻接表
空间复杂度	O(V²)	O(V + E)
添加边	O(1)	O(1)
删除边	O(1)	O(V) 最坏
查找边	O(1)	O(V) 最坏
遍历所有邻接顶点	O(V)	O(度数)
适用图类型	稠密图	稀疏图
内存使用	固定	动态
缓存友好性	好	一般

下面来给大家说一下图的遍历方式

深度优先搜索（DFS）

深度优先搜索（Depth-First Search，DFS）是图遍历的基本算法之一，它的特点是尽可能深地搜索图的分支。

DFS算法原理

基本思想

DFS的核心思想是：

从一个顶点开始访问
访问该顶点的一个未访问的邻接顶点
递归地对该邻接顶点执行DFS
如果没有未访问的邻接顶点，则回溯到上一个顶点
重复上述过程直到所有可达顶点都被访问

可以理解为尽可能深的找节点

就比如上面的 DFS序列，从 A 开始遍历的话，则可以是 ABDEC，ABCED

时间复杂度和空间复杂度

时间复杂度：O(V + E)，其中V是顶点数，E是边数
空间复杂度：O(V)，主要用于存储访问状态和递归栈

广度优先搜索

广度优先搜索（Breadth-First Search，BFS）是另一种基本的图遍历算法，与DFS不同，BFS采用"先访问邻居，再访问邻居的邻居"的策略。BFS特别适合求解最短路径、层次遍历等问题。

BFS算法原理

基本思想

BFS的核心思想是：

从起始顶点开始，将其加入队列
从队列中取出一个顶点并访问
将该顶点的所有未访问邻接顶点加入队列
重复步骤2-3直到队列为空

这个图的BFS 搜索序列为，ABCDE、ACBED

时间复杂度和空间复杂度

时间复杂度：O(V + E)，其中V是顶点数，E是边数
空间复杂度：O(V)，主要用于存储访问状态和队列

BFS的重要性质

层次性：BFS按照距离起始顶点的层次进行遍历
最短路径：在无权图中，BFS能找到最短路径（边数最少）
完整性：BFS能访问到所有与起始顶点连通的顶点

01、图

# 图的基本概念

# 图的定义和生活中的图

# 图的基本术语

# 图与其他数据结构的区别

# 图的分类

# 有向图 vs 无向图

# 加权图 vs 无权图

# 连通图 vs 非连通图

# 特殊类型的图

# 邻接矩阵存储

# 邻接矩阵的基本概念

# 邻接矩阵的实现方式

# 邻接矩阵的空间和时间复杂度分析

# 邻接矩阵的优缺点

# 邻接表存储

# 邻接表的基本概念

# 邻接表的空间和时间复杂度分析

# 邻接表 vs 邻接矩阵对比

# 深度优先搜索（DFS）

# DFS算法原理

# 基本思想

# 时间复杂度和空间复杂度

# 广度优先搜索

# BFS算法原理

# 基本思想

# 时间复杂度和空间复杂度

# BFS的重要性质

图的基本概念

图的定义和生活中的图

图的基本术语

图与其他数据结构的区别

图的分类

有向图 vs 无向图

加权图 vs 无权图

连通图 vs 非连通图

特殊类型的图

邻接矩阵存储

邻接矩阵的基本概念

邻接矩阵的实现方式

邻接矩阵的空间和时间复杂度分析

邻接矩阵的优缺点

邻接表存储

邻接表的基本概念

邻接表的空间和时间复杂度分析

邻接表 vs 邻接矩阵对比

深度优先搜索（DFS）

DFS算法原理

基本思想

时间复杂度和空间复杂度

广度优先搜索

BFS算法原理

基本思想

时间复杂度和空间复杂度

BFS的重要性质