4、翻转对

题目描述

leetcode 493 翻转对

给定一个数组 nums ，如果 i < j 且 nums[i] > 2*nums[j] 我们就将 (i, j) 称作一个重要翻转对。

你需要返回给定数组中的重要翻转对的数量。

示例 1:

输入: [1,3,2,3,1] 输出: 2

示例 2:

输入: [2,4,3,5,1] 输出: 3

题目解析

我们理解了逆序对的含义之后，题目理解起来完全没有压力的，这个题目第一想法可能就是用暴力法解决，但是会超时，所以我们有没有办法利用归并排序来完成呢？

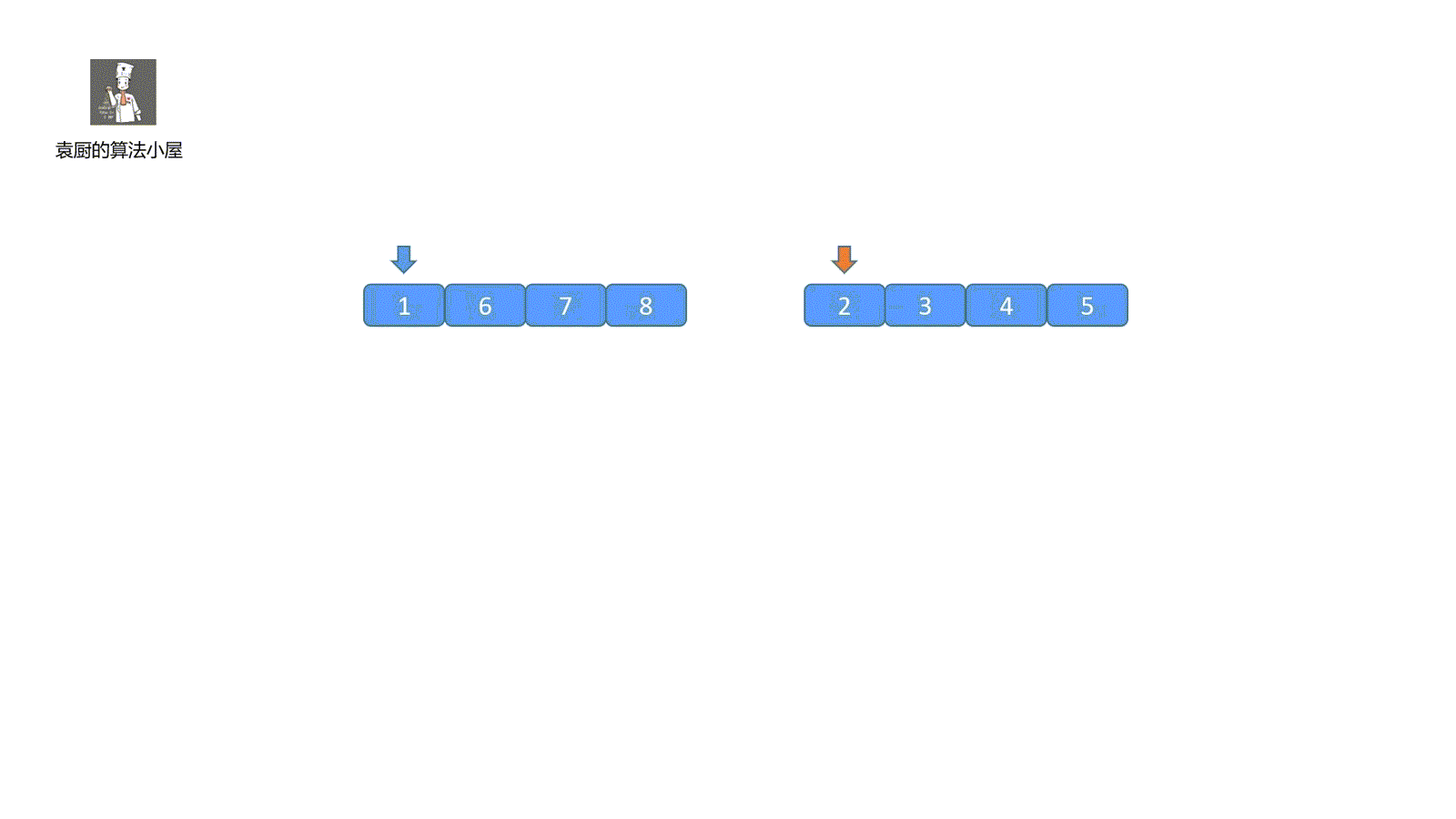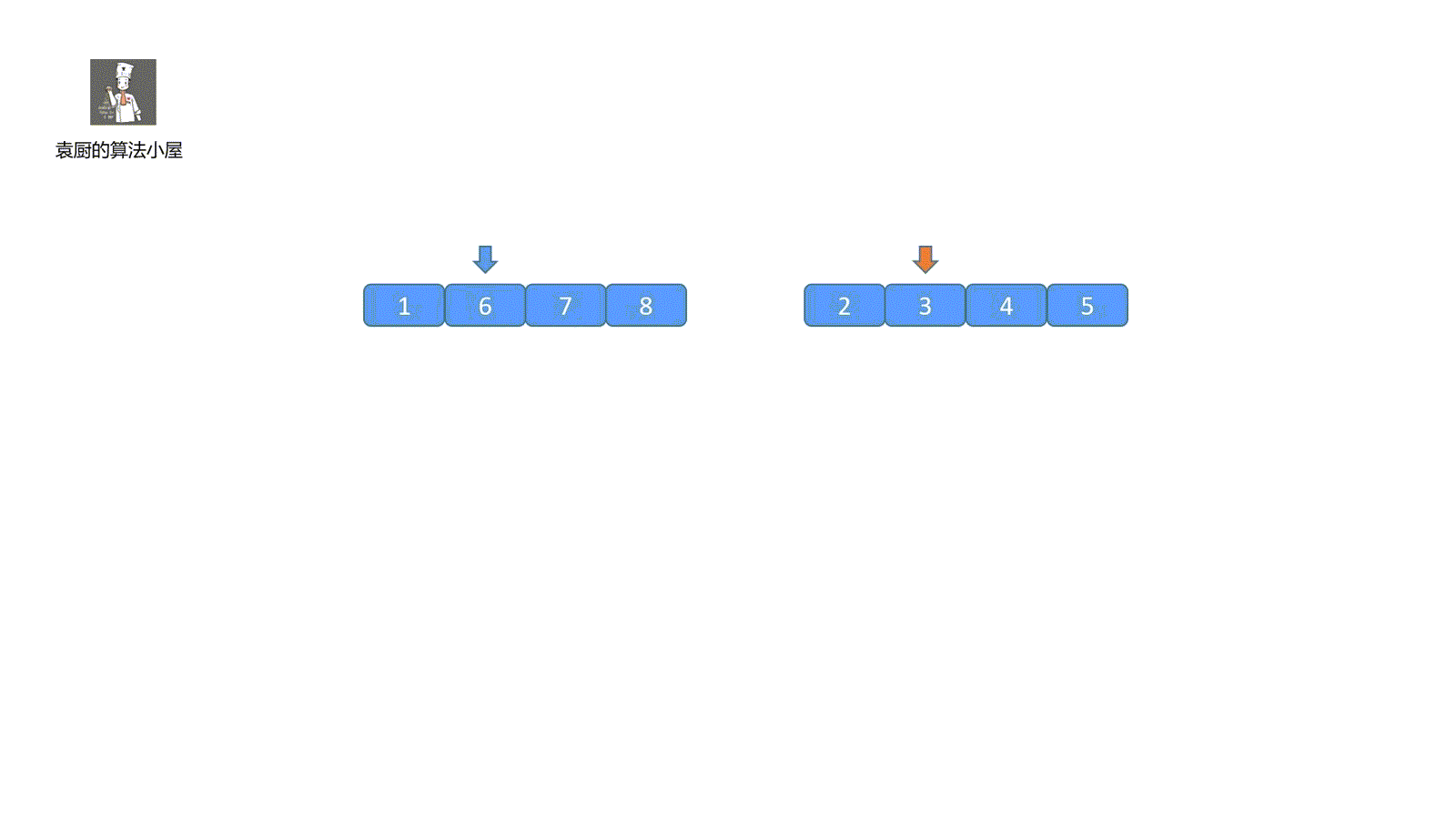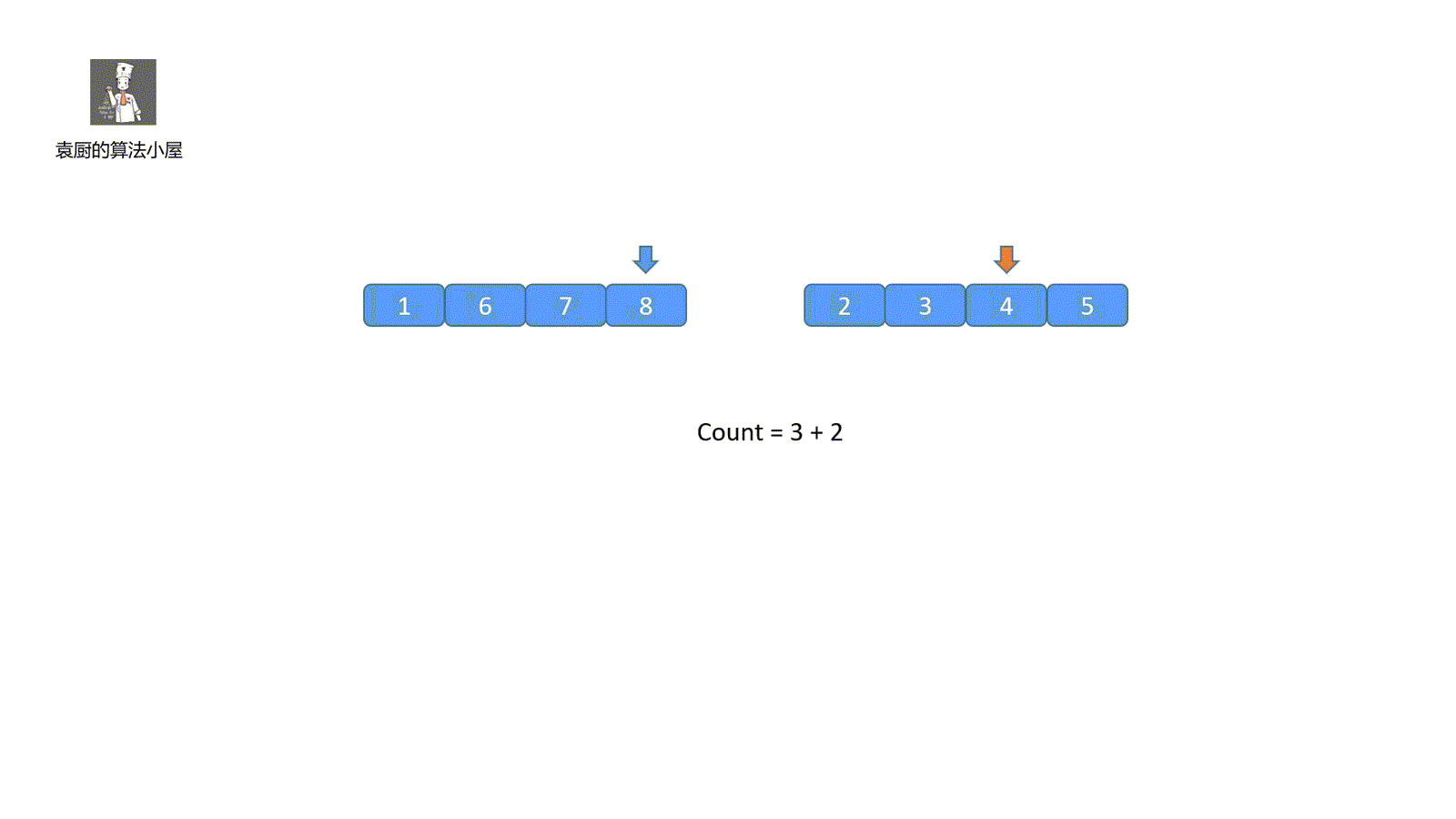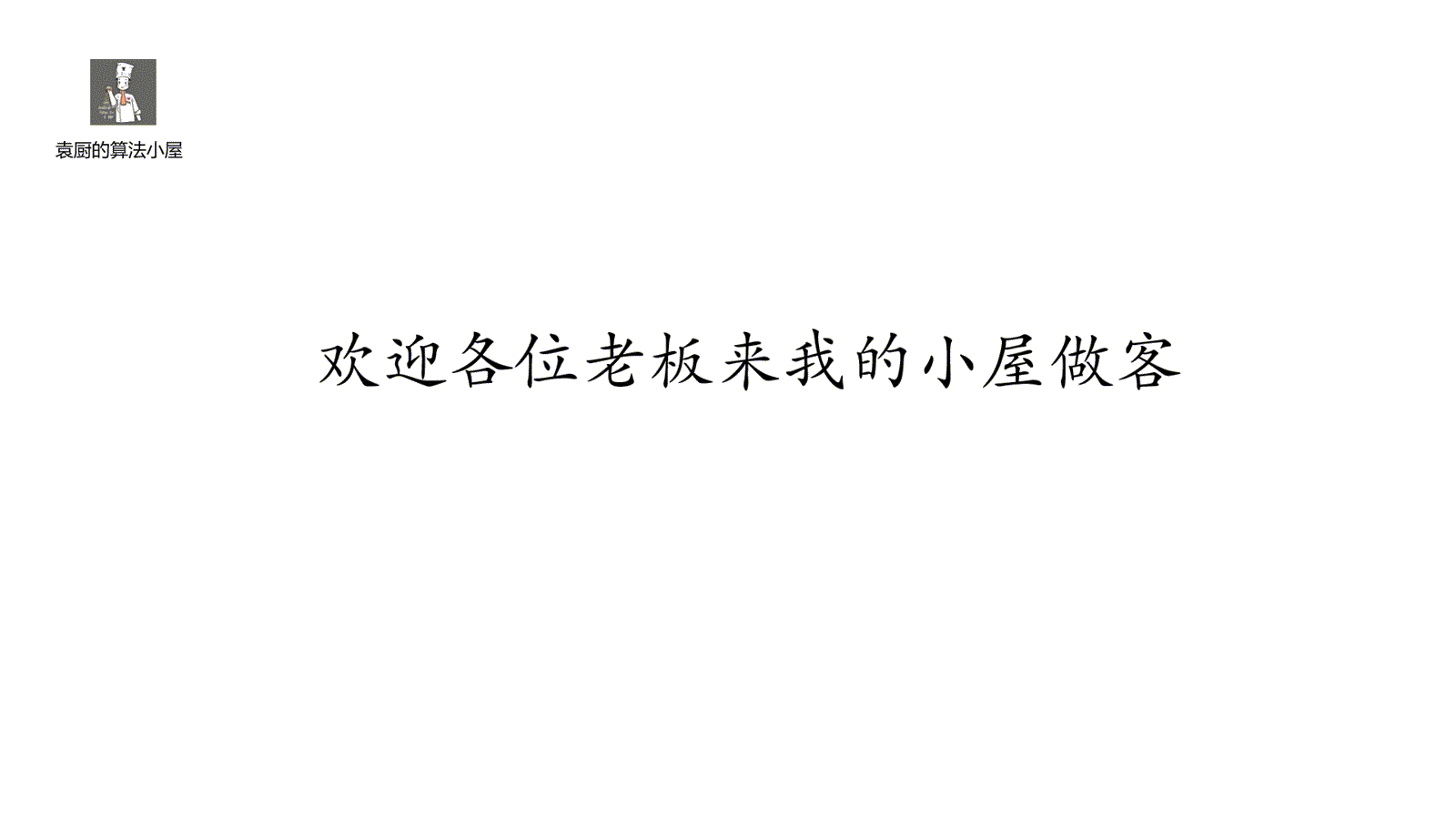
我们继续回顾一下归并排序的归并过程，两个小集合是有序的，然后我们需要将小集合归并到大集合中，则我们完全可以在归并之前，先统计一下翻转对的个数，然后再进行归并，则最后排序完成之后自然也就得出了翻转对的个数。具体过程见下图。

翻转对

此时我们发现 6 > 2 * 2，所以此时是符合情况的，因为小数组是单调递增的，所以 6 后面的元素都符合条件，所以我们 count += mid - temp1 + 1；则我们需要移动紫色指针，判断后面是否还存在符合条件的情况。

翻转对

我们此时发现 6 = 3 * 2，不符合情况，因为小数组都是完全有序的，所以我们可以移动红色指针，看下后面的数有没有符合条件的情况。这样我们就可以得到翻转对的数目啦。下面我们直接看动图加深下印象吧！

动画模拟

是不是很容易理解啊，那我们直接看代码吧，仅仅是在归并排序的基础上加了几行代码。

代码

#include <vector>
#include <algorithm>  // 用于std::copy

class Solution {
private:
    int count;  // 翻转对计数器，私有成员封装

    // 归并排序核心：合并两个有序区间并统计翻转对
    void mergeSort(std::vector<int>& nums, int left, int mid, int right) {
        // 临时数组存储合并结果，大小为区间长度
        std::vector<int> temparr(right - left + 1);
        int i = left;       // 左区间指针
        int j = mid + 1;    // 右区间指针
        int k = 0;          // 临时数组指针

        // 第一阶段：统计翻转对（nums[i] > 2 * nums[j]）
        while (i <= mid && j <= right) {
            // 使用long long防止乘法溢出，2LL确保运算为64位
            if (static_cast<long long>(nums[i]) > 2LL * nums[j]) {
                // 左区间剩余元素均满足条件，直接累加
                count += mid - i + 1;
                j++;  // 移动右指针
            } else {
                i++;  // 移动左指针
            }
        }

        // 重置指针，准备归并操作
        i = left;
        j = mid + 1;

        // 第二阶段：标准归并排序，合并两个有序区间
        while (i <= mid && j <= right) {
            if (nums[i] <= nums[j]) {
                temparr[k++] = nums[i++];
            } else {
                temparr[k++] = nums[j++];
            }
        }

        // 处理左区间剩余元素（使用标准库算法更规范）
        if (i <= mid) {
            std::copy(nums.begin() + i, nums.begin() + mid + 1, temparr.begin() + k);
        }

        // 处理右区间剩余元素
        if (j <= right) {
            std::copy(nums.begin() + j, nums.begin() + right + 1, temparr.begin() + k);
        }

        // 将合并结果写回原数组
        std::copy(temparr.begin(), temparr.end(), nums.begin() + left);
    }

    // 递归分割数组
    void merge(std::vector<int>& nums, int left, int right) {
        if (left < right) {  // 区间有效时才分割
            // 计算中间索引（避免left+right溢出）
            int mid = left + ((right - left) >> 1);
            merge(nums, left, mid);         // 左半部分递归
            merge(nums, mid + 1, right);    // 右半部分递归
            mergeSort(nums, left, mid, right);  // 合并并统计
        }
    }

public:
    // 计算数组中的翻转对数量
    int reversePairs(std::vector<int>& nums) {
        count = 0;  // 初始化计数器
        if (nums.size() < 2) {  // 边界处理：元素不足2个时无翻转对
            return 0;
        }
        merge(nums, 0, static_cast<int>(nums.size()) - 1);
        return count;
    }
};