8、缺失的第一个正数

题目描述

缺失的第一个正数

给你一个未排序的整数数组，请你找出其中没有出现的最小的正整数。

示例 1:

输入: [1,2,0] 输出: 3

示例 2:

输入: [3,4,-1,1] 输出: 2

示例 3:

输入: [7,8,9,11,12] 输出: 1

重复遍历

让我们找出缺失的最小正整数，而且这是一个未排序的数组，我们可以利用暴力求解，挨个遍历发现那个不存在直接返回即可。我们这里使用两种方法解决这个问题，大家也可以提出自己的做法。

我们既然是返回缺失的正整数，那么我们则可以将这个数组中的所有正整数保存到相应的位置，见下图。

微信截图_20210109135536

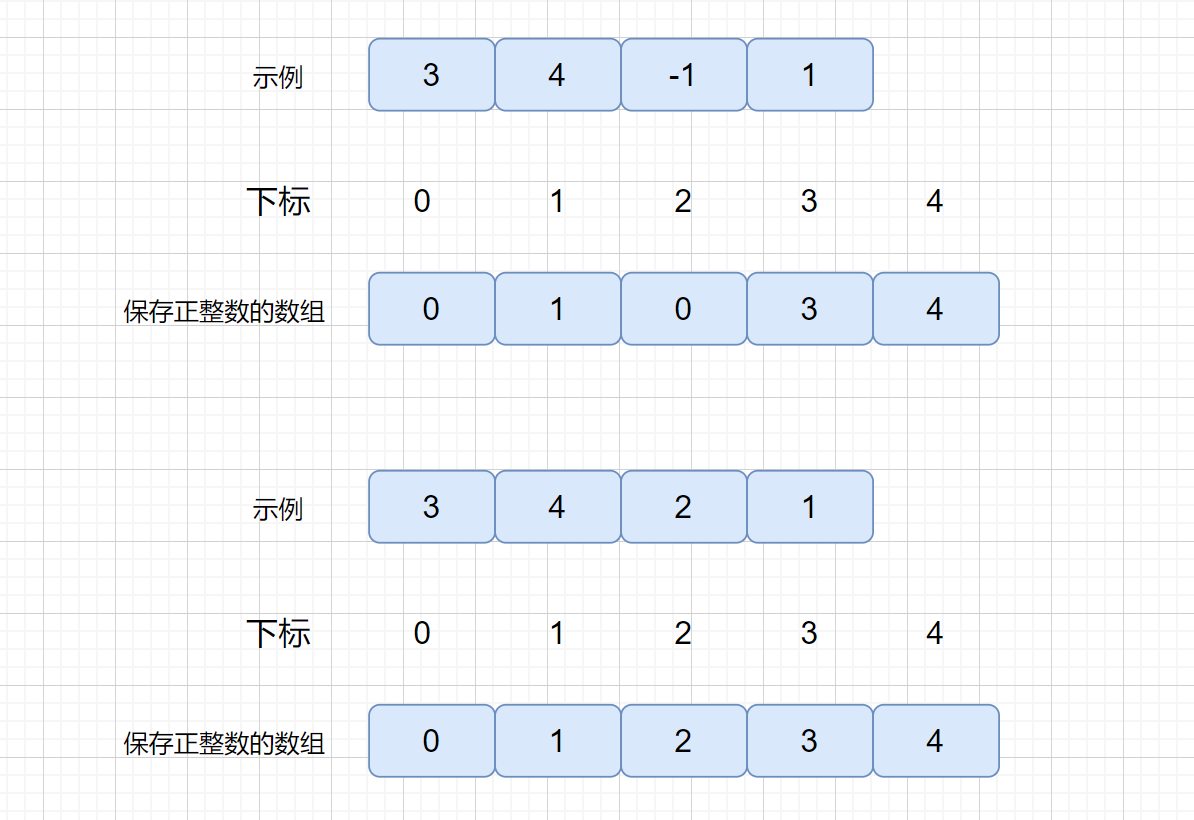
上图中，我们遍历一遍原数组，将正整数保存到新数组中，然后遍历新数组，第一次发现 newnum[i] != i 时，则说明该值是缺失的，返回即可，例如我上图中的第一个示例中的 2，如果遍历完新数组，发现说所有值都对应，说明缺失的是 新数组的长度对应的那个数，比如第二个示例中 ，新数组的长度为 5，此时缺失的为 5，返回长度即可，很容易理解。

注：我们发现我们新的数组长度比原数组大 1，是因为我们遍历新数组从 1，开始遍历。

动图解析

代码

Java Code:

class Solution {
    public int firstMissingPositive(int[] nums) {
        if (nums.length == 0) {
            return 1;
        }
        //因为是返回第一个正整数，不包括 0，所以需要长度加1，细节1
        int[] res = new int[nums.length + 1];
        //将数组元素添加到辅助数组中
        for (int x : nums) {
            if (x > 0 && x < res.length) {
               res[x] = x;
            }
        }
        //遍历查找,发现不一样时直接返回
        for (int i = 1; i < res.length; i++) {
            if (res[i] != i) {
                return i;
            }
        }
        //缺少最后一个，例如 1，2，3此时缺少 4 ，细节2
        return res.length;
    }
}

C++ Code:

#include <vector>
using namespace std;

class Solution {
public:
    int firstMissingPositive(vector<int>& nums) {
        // 处理空数组情况：空数组缺失的第一个正整数是1
        if (nums.empty()) {
            return 1;
        }
        
        // 辅助数组：长度为原数组长度+1（确保能覆盖到可能的最大候选值n，n为原数组长度）
        int n = nums.size();
        vector<int> res(n + 1, 0);  // 初始化为0，对应Java中int数组的默认值0
        
        // 将原数组中的有效正整数（1~n范围内）映射到辅助数组
        for (int x : nums) {
            // 只处理正整数，且范围在1~n之间（超出范围的正整数不影响结果）
            if (x > 0 && x < res.size()) {  // res.size() = n+1，即x <= n
                res[x] = x;  // 位置x存储值x，标记该正整数存在
            }
        }
        
        // 从1开始遍历辅助数组，寻找第一个未被标记的位置（res[i] != i）
        for (int i = 1; i < res.size(); ++i) {
            if (res[i] != i) {
                return i;  // 找到缺失的第一个正整数
            }
        }
        
        // 若1~n均存在，则缺失的是n+1（例如数组为[1,2,3]时，缺失4）
        return res.size();
    }
};

原地置换

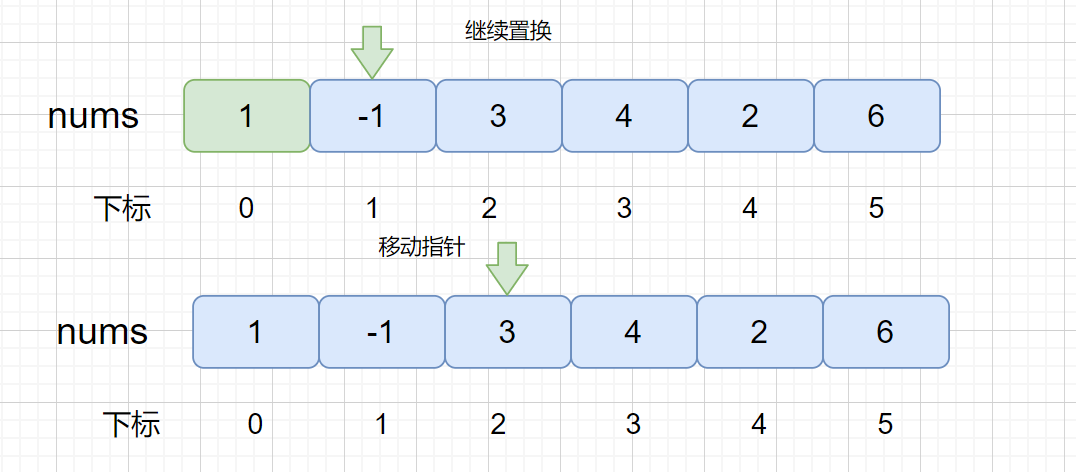
我们通过上面的例子了解这个解题思想，我们有没有办法不使用辅助数组完成呢？我们可以使用原地置换，直接在 nums 数组内，将值换到对应的索引处，与上个方法思路一致，只不过没有使用辅助数组，理解起来也稍微难理解一些。

下面我们看一下原地置换的一些情况。

注：红色代表待置换，绿色代表置换完毕

置换1

置换2

动图解析

原地置换

代码

Java Code:

class Solution {
    public int firstMissingPositive(int[] nums) {
        int len = nums.length;
        if (len == 0) {
            return 1;
        }
        for (int i = 0; i < len; ++i) {
            //需要考虑指针移动情况，大于0，小于len+1，不等与i+1，两个交换的数相等时，防止死循环
            while (nums[i] > 0 && nums[i] < len + 1 && nums[i] != i+1 && nums[i] != nums[nums[i]-1]) {
                swap(nums,i,nums[i] - 1);
            }
        }
        //遍历寻找缺失的正整数
        for (int i = 0; i < len; ++i) {
            if(nums[i] != i+1) {
                return i+1;
            }
        }
        return len + 1;
    }
    //交换
   public void swap(int[] nums, int i, int j) {
        if (i != j) {
            nums[i] ^= nums[j];
            nums[j] ^= nums[i];
            nums[i] ^= nums[j];
        }
    }
}

C++ Code

class Solution
{
public:
    int firstMissingPositive(vector<int> &nums)
    {
        int size = nums.size();
        //判断范围是否符合要求
        auto inRange = [](auto s, auto e)
        {
            return [s, e](auto &n)
            {
                return e >= n && n >= s;
            };
        };
        auto cusInRange = inRange(1, size);
        //增加数组长度, 便于计算, 不需要再转换
        nums.push_back(0);

        for (int i = 0; i < size; i++)
        {
            //将不在正确位置的元素放到正确位置上
            while (cusInRange(nums[i]) && nums[i] != i && nums[nums[i]] != nums[i])
            {
                swap(nums[i], nums[nums[i]]);
            }
        }

        //找出缺失的元素
        for (int i = 1; i <= size; i++)
        {
            if (nums[i] != i)
                return i;
        }
        return size + 1;
    }
};